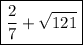Question

What much expression represents a rational number?

Answer 1

`\displaystyle (2)/(7)+√(121)`

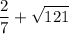
Explanation:

Rational Numbers

A rational number is any number that can be expressed as a fraction

`\displaystyle (a)/(b), \ b\\eq 0`

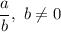
for a and b any integer and b different from 0.

As a consequence, any number that cannot be expressed as a fraction or rational number is defined as an Irrational number.

Let's analyze each one of the given options

`\displaystyle (5)/(9)+√(18)`

The first part of the number is indeed a rational number, but the second part is a square root whose result cannot be expressed as a rational, thus the number is not rational

`\pi + √(16)`

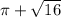
The second part is an exact square root (resulting 4) but the first part is a known irrational number called pi. It's not possible to express pi as a fraction, thus the number is irrational

`\displaystyle (2)/(7)+√(121)`

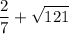
The square root of 121 is 11. It makes the whole number a sum of a rational number plus an integer, thus the given number is rational

`\displaystyle (3)/(10)+√(11)`

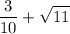
As with the first number, the square root is not exact. The sum of a rational number plus an irrational number gives an irrational number.

Correct option:

`\boxed{\displaystyle (2)/(7)+√(121)}`