Answer: Choice B
Matthew will score less than 27 points in about 0.15% of his basketball games.
=======================================================
Step-by-step explanation:
mu = 33 = population mean
sigma = 2 = population standard deviation
Let's find the z score when x = 27
z = (x - mu)/sigma
z = (27-33)/2
z = -6/2
z = -3
A score of 27 points is exactly three standard deviation units below the mean of 33 points.
Now refer to the Empirical Rule chart shown below. Notice that roughly 99.7% of the entire population is within 3 standard deviations of the mean. This is the span from z = -3 to z = 3.
That leaves about 100% - 99.7% = 0.3% left over for the two tails combined.
One tail has about (0.3%)/2 = 0.15% of the total area, and therefor about 0.15% of the total games will have Matthew scoring less than 27 points. This is an estimate of course.
To get a more accurate answer, you can use a Z table to find that
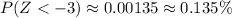
which isn't too far off from the 0.15%