Question

I’m the circle be, CE equals 13.5. Find BD. Round to the nearest hundredth

Answer 1

Given:

CE = 13.5

AB = 8

To find:

The length of BD.

Solution:

AB and BF are radius of the circle.

BF = 8

Radius BF is perpendicular to the chord CE.

Therefore it BF bisects the chord.

CD =
`(1)/(2) (13.5)=6.75`

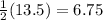
Draw radius BC to complete right triangle BCD.

BC = 8 units

Using Pythagorean Theorem:

`B D^(2)+C D^(2)=B C^(2)`

`B D^(2)+6.75^(2)=8^(2)`

`B D^(2)+45.5625=64`

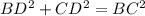
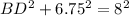
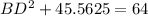
Subtract 45.5625 from both sides.

`B D^(2)=18.4375`

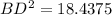
Taking square root on both sides, we get

`B D \approx 4.29`

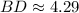
The length of BD is 4.29 units.