Question

PLZ HELP ALGEBRA!!!!
AND PLZ SHOW WORK

Answer 1

Explanation:

n is the number of times the interest compounds per year. If the interest in this problem only compounds once per year ("annually"), then n = 1 and you'd be just as well off to use the formula:

`A=P(1+r)^t`

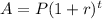
When n = 1, r/n is just r. But I'll show you using the formula they want you to use; it's the same anyways.

For us, P = 500, r = .015, n = 1. Filling that into the formula:

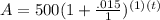`A=500(1+(.015)/(1))^((1)(t))` which simplifies down to

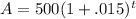`A=500(1+.015)^t` and

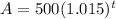`A=500(1.015)^t` (see what I meant about not having to use the formula with "n" in it if n 1?)

That formula is the answer to part a. For part b, we are to find how long it takes for the account to reach $800. $800 goes in for A:

`800=500(1.015)^t`

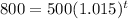
Begin by dividing both sides by 500 to get:

`1.6=(1.015)^t`

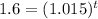
The only way to bring that t down from its current exponential position is to take the natural log of both sides. I will do that and at the same time apply the power rule for logs which says the exponent will come down out in front of the log:

`ln(1.6)=tln(1.015)`

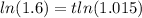
Divide both sides by ln(1.015):

`(ln(1.6))/(ln(1.015))=t`

Do this on your calculator to find that

t = 31.5 years