Option B:
ASA congruence
Solution:
Step 1: Given
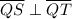
Step 2: Given
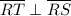
Step 3: Given
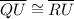 (Included side)
(Included side)
Step 4: All right angles are congruent.
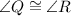 (Angle)
(Angle)
Step 5: By vertical angle theorem
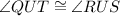 (Angle)
(Angle)
Step 6: By ASA congruence
QU and RU are included side of corresponding angles.
Therefore by ASA congruence rule,
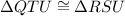
Option B is the correct answer.
Hence proved.