Question

Suppose the mean income of firms in the industry for a year is 95 million dollars with a standard deviation of 5 million dollars. If incomes for the industry are distributed normally, what is the probability that a randomly selected firm will earn less than 100 million dollars

Answer 1

Probability that a randomly selected firm will earn less than 100 million dollars is 0.8413.

Explanation:

We are given that the mean income of firms in the industry for a year is 95 million dollars with a standard deviation of 5 million dollars. Also, incomes for the industry are distributed normally.

Let X = incomes for the industry

So, X ~ N(
`\mu=95,\sigma^(2)=5^(2)`)

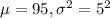Now, the z score probability distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean income of firms in the industry = 95 million dollars

`\sigma` = standard deviation = 5 million dollars

So, probability that a randomly selected firm will earn less than 100 million dollars is given by = P(X < 100 million dollars)

P(X < 100) = P(
`(X-\mu)/(\sigma)` <
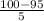`(100-95)/(5)` ) = P(Z < 1) = 0.8413 {using z table]

Therefore, probability that a randomly selected firm will earn less than 100 million dollars is 0.8413.