Question

John Lester is at the park practicing his pitching. Since he doesn’t have a catcher, John wants to pitch the ball all the way around the Earth so he can catch it himself. Neglecting air drag and any obstacles that might be in the way, about how fast must the ball be moving? You may take the radius of the Earth to be 6400 km.

Answer 1

`v_(o) = 79.314* 10^(6)\,(m)/(s)`

Step-by-step explanation:

Let assume that John Lester has a height of 1.80 meters and throws the ball at 70 percent of John Lester's height. The time before the ball hits the soil is:

`0\,m = 0.7\cdot (1.80\,m) -(1)/(2)\cdot (9.807\,(m)/(s^(2)) )\cdot t^(2)`

`t \approx 0.507\,s`

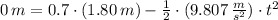
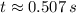
The initial horizontal velocity required to pitch the ball all the way around the Earth is:

`2\pi\cdot (6.4* 10^(6)\,m)= v_(o)\cdot (0.507\,s)`

`v_(o) = 79.314* 10^(6)\,(m)/(s)`