Question

For one binomial experiment, n1 = 75 binomial trials produced r1 = 30 successes. For a second independent binomial experiment, n2 = 100 binomial trials produced r2 = 50 successes. At the 5% level of significance, test the claim that the probabilities of success for the two binomial experiments differ.

Answer 1

There is no enough evidence that the probabilities of success for the two binomial experiments differ.

Explanation:

The null and alternative hypothesis are:

`H_0: p_2-p_1=0\\\\H_a: p_2-p_1\\eq0`

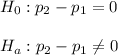
The significance level is 0.05.

The proportion of the first experiment is p_1=30/75=0.4.

The proportion of the second experiment is p_2=50/100=0.5.

The difference between proportions is

`\Delta p=p_2-p_1=0.5-0.4=0.1`

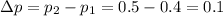
The standard deviation of the difference between the proportion is:

`\sigma=\sqrt{(p_2(1-p_2))/(n_2)+(p_1(1-p_1))/(n_1) } \\\\ \sigma=\sqrt{(0.5*0.5)/(100)+(0.4*0.6)/(75) } \\\\ \sigma=√(0.0057)=0.075`

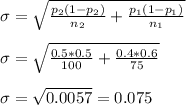
Then, the z-statistic is:

`z=(\Delta p)/(\sigma)=(0.1)/(0.075) =1.33`

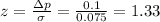
The p-value for this two-sided test is P(z>1.33)=0.09. This is bigger than the significance level, so the effect is not significant.

There is no enough evidence that the probabilities of success for the two binomial experiments differ.