Answer:
The temperature coefficient of resistivity is 0.001689 /°C
Step-by-step explanation:
Given initial temperature
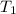 = 25°C = 25 + 273 = 298 k
= 25°C = 25 + 273 = 298 k
The final temperature
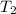 = Three times
= Three times
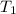 = 3
= 3
Resistance at
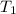 =
=
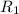
Resistance at
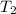 (
(
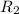 )= double resistance at
)= double resistance at
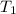 = 2
= 2
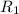
The resistance of a body can be obtained when given the above parameters with the expression below;
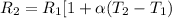 ...............................1
...............................1
Inputting the parameters into equation 1 we have;
2
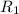 =
=
isolating α we have;
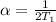
α = 1/(2 x 298 k)
α = 1/596
α = 0.001678 /K = 0.001689 /°C (change in temperature is the same at both centigrade and kelvin scale.
Therefore the temperature coefficient of resistivity is
0.001689 /°C