Question

The following sample of heights was taken from 5 air filters off the assembly line. Construct the 80% confidence interval for the population variance for all air filters that come off the assembly line. Round your answers to two decimal places. 3.8,4.3,3.8,4.5,3.6

Answer 1

80% confidence interval for the population variance = (0.07 , 0.55).

Explanation:

We are given that the following sample of heights was taken from 5 air filters off the assembly line;

3.8, 4.3, 3.8, 4.5, 3.6

So, firstly the pivotal quantity for 80% confidence interval for the population variance is given by;

P.Q. =
`((n-1)s^(2) )/(\sigma^(2) )` ~
`\chi^(2) __n_-_1`

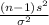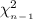
where, s = sample standard deviation

`\sigma` = population standard deviation

n = sample of rods = 5

Also,
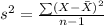`s^(2) = (\sum (X-\bar X)^(2) )/(n-1)` , where X = individual data value

`\bar X` = mean of data values = 4

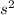`s^(2)` = 0.145

So, 80% confidence interval for population variance,
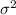`\sigma^(2)` is;

P(1.064 <
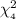`\chi^(2) __4` < 7.779) = 0.80 {As the table of
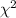`\chi^(2)` at 4 degree of freedom

gives critical values of 1.064 & 7.779}

P(1.064 <
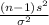`((n-1)s^(2) )/(\sigma^(2) )` < 7.779) = 0.80

P(
`( 1.064)/((n-1)s^(2) )` <
`(1 )/(\sigma^(2) )` <
`( 7.779)/((n-1)s^(2) )` ) = 0.80

P(
`( (n-1)s^(2))/(7.779 )` <
`\sigma^(2)` <
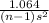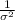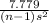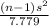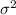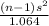`( (n-1)s^(2))/(1.064 )` ) = 0.80

80% confidence interval for
`\sigma^(2)` = (
`( (n-1)s^(2))/(7.779 )` ,
`( (n-1)s^(2))/(1.064 )` )

= (
`( (5-1)* 0.145)/(7.779 )` ,
`( (5-1)* 0.145)/(1.064 )` )

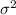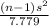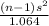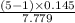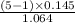= (0.07 , 0.55)

Therefore, 80% confidence interval for the population variance for all air filters that come off the assembly line is (0.07 , 0.55).