Answer:
Explanation:
Let's start out with the formulas for the volumes of the cone and the sphere.
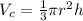 and
and
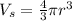
We are given that height of the cone is 8 and the radius of the sphere is 7. We are also told then that the volume of the cone is 2 times the volume of the sphere, which algebraically, looks like this:
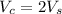 so let's set up our equation like that then, shall we?
so let's set up our equation like that then, shall we?
![(1)/(3)\pi r^2(8)=2[(4)/(3)\pi (7)^3]](https://img.qammunity.org/2021/formulas/mathematics/high-school/9k6hj1e8ylelwc3k7i32tlk3uxhdanu6mu.png) Let's simplify that a bit:
Let's simplify that a bit:
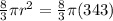
The reason for that is because it's apparent now that the 8/3 cancel each other out, as does the π, leaving us simply with:
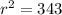
Take the square root of both sides to get that
r = 18.52 in.
Not sure how much you need to round.