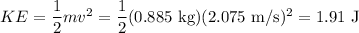Answer:
(a) Period = 0.436 s, frequency = 2.29 Hz
(b) 0.157 m
(c) 32.6 m/s²
(d) 2.26 J
(e) 1.91 J
Step-by-step explanation:
This is s simple harmonic motion in the form of a loaded spring. The initial velocity is the maximum velocity because the maximum velocity occurs at the equilibrium point.
Given:
Mass, m = 885 g = 0.885 kg
Spring constant, k = 184 N/m
Maximum velocity,
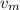 = 2.26 m/s
= 2.26 m/s
(a) Period, T, is given by:
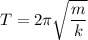
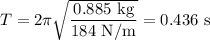
Frequency, f, is given by
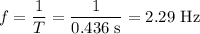
(b) The maximum velocity is related to the amplitude by
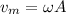
where A is the amplitude ω is the angular velocity and is given by

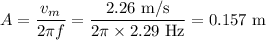
(c) Maximum acceleration is given by
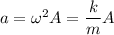

(d) Because the total energy is equal at any time, we determine the energy at equilibrium.
At equilibrium, displacement is 0 m and velocity is maximum. Hence, the potential energy is 0 J and the kinetic is maximum which is determined thus:
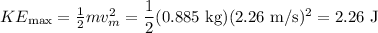
The maximum energy is 2.26 J.
(e) The velocity at any point is
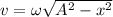
At point x = 4A,
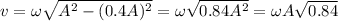
Putting the values of A and ω,
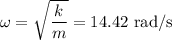
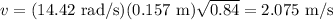
The kinetic energy is