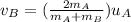Question

If we push one cart (Cart A) into a second stationary cart (Cart B), v_Ai is nonzero and v_Bi=0, respectively. Assume no outside forces will be involved and the collision is elastic (i.e. both momentum and kinetic energy are conserved). Derive the general equation for the velocity of Cart A after the collision v_Af as well as the velocity of Cart B after the collision v_Bf. We want these to be in terms of known quantities: initial velocity v_Ai and the mass of the carts m_A and m_B. Refer to the "Useful Theory" section below to get you started. If you get stuck, work with your lab partners and refer to your text to find the solution before

Answer 1

`v_A=((m_A-m_B)/(m_A+m_B))u_A`

`v_B=((2m_A)/(m_A+m_B))u_A`

Step-by-step explanation:

In an elastic collision, the total momentum of the system and the total kinetic energy of the system are conserved.

So:

- Conservation of momentum:

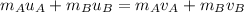`m_A u_A+m_B u_B = m_A v_A + m_B v_B` (1)

where

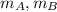`m_A, m_B` are the masses of cart A and B

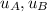`u_A,u_B` are the initial velocities of cart A and B

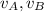`v_A,v_B` are the final velocities of cart A and B

- Conservation of kinetic energy:

`(1)/(2)m_A u_A^2+(1)/(2)m_B u_B^2= (1)/(2)m_A v_A^2 +(1)/(2) m_B v_B^2` (2)

From (1) we can write:

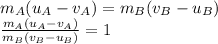`m_A (u_A-v_A)=m_B(v_B-u_B)\\(m_A (u_A-v_A))/(m_B(v_B-u_B))=1` (3)

From (2) we get:

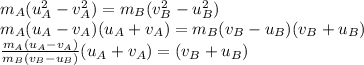`m_A (u_A^2-v_A^2)=m_B(v_B^2-u_B^2)\\m_A(u_A-v_A)(u_A+v_A)=m_B(v_B-u_B)(v_B+u_B)\\(m_A(u_A-v_A))/(m_B(v_B-u_B))(u_A+v_A)=(v_B+u_B)` (4)

Substituting (3) into (4),

`1\cdot (u_A+v_A)=(v_B+u_B)\\v_B=u_A+v_A-u_B` (5)

And substituting (5) into (1),

`m_A(u_A-v_A)=m_B (u_A+v_A-2u_B)`

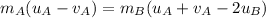
And now we can solve to find the final expressions:

`v_A=((m_A-m_B)/(m_A+m_B))u_A+((2m_B)/(m_A+m_B))u_B`

`v_B=((2m_A)/(m_A+m_B))u_A+((m_B-m_A)/(m_A+m_B))u_B`

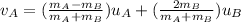
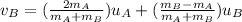
But in this problem

`u_B=0`

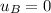
So the equations can be rewritten as

`v_A=((m_A-m_B)/(m_A+m_B))u_A`

`v_B=((2m_A)/(m_A+m_B))u_A`