Question

A record turntable is rotating at 33 rev/min. A watermelon seed is on the turntable 6.2 cm from the axis of rotation. (a) Calculate the acceleration of the seed, assuming that it does not slip. (b) What is the minimum value of the coefficient of static friction between the seed and the turntable if the seed is not to slip

Answer 1

To develop this problem we will apply the concepts related to the angular motion kinematic equations, as well as the concepts related to the balance of Forces (Friction and Newton's second law).

We will convert the angular velocity values into international units therefore

`\omega = 33 rev/min`

`\omega = 33(rev)/(min) ((2\pi rad)/(1 rev))((1 min)/(60s))`

`\omega = 3.455rad/s`

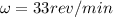
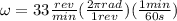
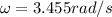
PART A)

Centripetal acceleration is defined as the product between the radius and the square of the angular velocity, then

`a = \omega^2 * r`

`a = (3.455)^2 (6.2*10^(-2))`

`a = 0.740096m/s^2`

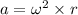
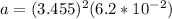
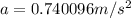
PART B) The friction force must be equivalent to the centripetal force (in Terms of the Newton's second law) to maintain balance therefore,

Frictional Force:

`F_f = \mu mg`

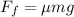
Centripetal force

`F_c = ma`

Equating the equations we will have,

`\mu mg = ma`

`\mu = (a)/(g)`

`\mu = (0.740096)/(9.8)`

`\mu = 0.075`

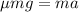
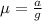
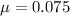
Therefore the minimum value of the coefficient of static fricton will be 0.075