Answer:
The minimum sample size is n=51.
Explanation:
The question is incomplete. The standard deviation is needed to calculate the sample size. It is estimated a standard deviation of 0.1 and mean 1.
Then the maximum margin of error is 0.0275, relative to the mean.
We can define the margin of error as the product of the z-value and the standard deviation, divided by the square root of the sample size.

The z-value for a 95% confidence interval is z=1.960.
The standard deviation is 1.
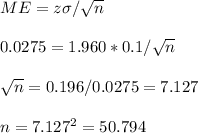
The minimum sample size is n=51.