Question

Willow Brook National Bank operates a drive-up teller window that allows customers to complete bank transactions without getting out of their cars. On weekday mornings, arrivals to the drive-up teller window occur at random, with an arrival rate of 24 customers per hour or 0.4 customers per minute. What is the mean or expected number of customers that will arrive in a five-minute period? λ = per five minute period Assume that the Poisson probability distribution can be used to describe the arrival process. Use the arrival rate in part (a) and compute the probabilities that exactly 0, 1, 2, and 3 customers will arrive during a five-minute period. Round your answers to four decimal places. x P(x) 0 1 2 3 Delays are expected if more than three customers arrive during any five-minute period. What is the probability that delays will occur? Round your answer to four decimal places. P(Delay Problems) =

Answer 1

(a) λ = 2.

(b) P (X = 0) = 0.1353; P (X = 1) = 0.2706;

P (X = 2) = 0.2706; P (X = 3) = 0.1804

(c) P (Delay Problems) = 0.1431.

Explanation:

Let X = number of arrivals at the drive-up teller window.

The average number of arrivals at the drive-up teller window per minute is,

p = 0.4 customers/ minute.

(1)

Compute the expected number of customers at the drive-up teller window in n = 5 minutes as follows:

`E(X)=\lambda\\=np\\=5* 0.4\\=2`

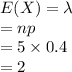
Thus, the mean number of customers that will arrive in a five-minute period is λ = 2.

(2)

The random variable X follows a Poisson distribution with parameter λ = 2.

The probability mass function of X is:

`P(X=x)=(e^(-2)2^(x))/(x!);\ x=0,1,2,3...`

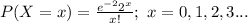
Compute the probability of exactly 0 arrivals in 5 minutes as follows:

`P(X=0)=(e^(-2)2^(0))/(0!)=(0.1353* 1)/(1)=0.1353`

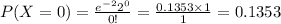
Compute the probability of exactly 1 arrivals in 5 minutes as follows:

`P(X=1)=(e^(-2)2^(1))/(1!)=(0.1353* 2)/(1)=0.2706`

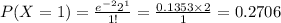
Compute the probability of exactly 2 arrivals in 5 minutes as follows:

`P(X=2)=(e^(-2)2^(2))/(2!)=(0.1353* 4)/(2)=0.2706`

Compute the probability of exactly 3 arrivals in 5 minutes as follows:

`P(X=3)=(e^(-2)2^(3))/(3!)=(0.1353* 8)/(6)=0.1804`

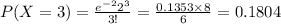
Thus, the values are:

P (X = 0) = 0.1353

P (X = 1) = 0.2706

P (X = 2) = 0.2706

P (X = 3) = 0.1804

(3)

Delays occur in the service time if there are more than three customers arrive during any five-minute period.

Compute the probability that there are more than 3 customers as follows:

P (X > 3) = 1 - P (X ≤ 3)

`=1-\sum\limits^(3)_(x=0){(e^(-2)2^(x))/(x!)}\\=1-(0.1353+0.2706+0.2706+0.1804)\\=1-0.8569\\=0.1431`

Thus, the probability that delays will occur is 0.1431.