Answer:
The expressions which equivalent to
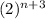 are:
are:
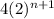 ⇒ B
⇒ B
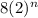 ⇒ C
⇒ C
Explanation:
Let us revise some rules of exponent
Now let us find the equivalent expressions of
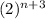
A.
∵ 4 = 2 × 2
∴ 4 =
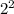
∴
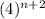 =
=

- By using the second rule above multiply 2 and (n + 2)
∵ 2(n + 2) = 2n + 4
∴
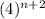 =
=
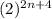
B.
∵ 4 = 2 × 2
∴ 4 = 2²
∴
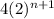 = 2² ×
= 2² ×
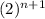
- By using the first rule rule add the exponents of 2
∵ 2 + n + 1 = n + 3
∴
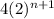 =
=
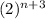
C.
∵ 8 = 2 × 2 × 2
∴ 8 = 2³
∴
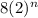 = 2³ ×
= 2³ ×
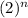
- By using the first rule rule add the exponents of 2
∵ 3 + n = n + 3
∴
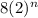 =
=
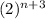
D.
∵ 16 = 2 × 2 × 2 × 2
∴ 16 =
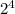
∴
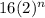 =
=
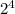 ×
×
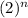
- By using the first rule rule add the exponents of 2
∵ 4 + n = n + 4
∴
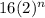 =
=
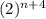
E.
 is in its simplest form
is in its simplest form
The expressions which equivalent to
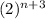 are:
are:
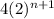 ⇒ B
⇒ B
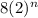 ⇒ C
⇒ C