Question

2. A 3.6 mH inductor with negligible resistance has a 1.0 A current through it. The current starts to increase at t = 0 s, creating a constant 5.0 mV voltage across the inductor. How much charge passes through the inductor between t = 0 s and t = 5.0 s?

Answer 1

To solve this problem it will be necessary to apply the concepts related to the electric potential in terms of the variation of the current and inductance. From this definition, we will start to find the load, which is dependent on the current as a function of time.

`\Delta V = L (dI)/(dt)`

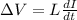
Here,

L = Inductance

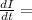`(dI)/(dt) =` Rate of change of current

If we take the equation and put the variation of the current as a function of time, in terms of the voltage in terms of the inductance we would have

`(dI)/(dt) = (\Delta V)/(L)\\(dI)/(dt) = (5.0mV)/(3.6mH)\\(dI)/(dt) = 1.389A/s`

The current as a function of time will be then,

`I(t) = I_0 + ((dI)/(dt))t\\I(t) = I_0 + ((\Delta V)/(L))t`

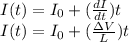
The charge is the integral of the current in each variation of the time, then

`Q = \int (I(t)) dt`

Equation the terms we will have,

`Q = \int_0^t (I_0 + ((\Delta V)/(L))t) dt \\Q = \bigg[I_0t + (1)/(2)(\Delta V)/(L)t^2\bigg]^(5.0s)_(0s)\\Q = (1) (5.0s)+(1)/(2) (1.389A/s)(5.0s)^2 \\Q = 22C`