Question

Consider a machine that fills 275 gallon tanks of water. The owner discovers that the machine does not always dispense exactly 275 gallons. Instead, they discover that it fills between 272 and 275 gallons. 25% of the time it will fill between 272 and 273 gallons of water, 20% of the time it fills between 273 and 274 gallons, and 55% of the time it fills between 274 and 275 gallons. (a) What is the random variable? Is this discrete or continuous? (b) If the variable is discrete, state the sample space. If the variable is continuous, give the density curve. (c) What is the probability that a 275 gallon tank gets less than 272.5 gallons or more than 273.8 gallons of water?

Answer 1

(a) The random variable X is a continuous random variable.

(b) The probability density function is shown below.

(c) The probability that a 275 gallon tank gets less than 272.5 gallons or more than 273.8 gallons of water is 0.285.

Explanation:

Let the random variable X be denoted as the amount of water filled by the machine in a 275 gallon tank.

(a)

The random variable X is a continuous random variable.

A continuous random variables assumes infinite values. That is, they assume values in a fixed interval. For example, the distance covered by a car.

A discrete random variable assumes fixed definite values. They assume whole number values. For example, number of customers visiting a bank in an hour.

The amount of water in the tank can be any value between 0 to 275 gallon.

Hence, the random variable X is a continuous random variable.

(b)

The probability density function of the continuous random variable X is given as follows:

`0.25;\ 272<X<273`

`f_(X)(x) =0.20;\ 273<X<274`

`0.55;\ 274<X<275`

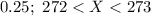
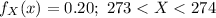
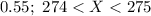
(c)

Compute the value of P (272.5 < X < 273.8) as follows:

`P(272.5<X<273.8)=\int\limits^(273)_(272.5) {f(x)} \, dx+\int\limits^(273.8)_(273) {f(x)} \, dx \\=0.25* [273-272.5]+0.20* [273.8-273]\\=0.125+0.16\\=0.285`

Thus, the probability that a 275 gallon tank gets less than 272.5 gallons or more than 273.8 gallons of water is 0.285.