Question

The weights of 67 randomly selected axles were found to have a variance of 3.85. Construct the 80% confidence interval for the population variance of the weights of all axles in this factory. Round your answers to two decimal places.

Answer 1

`3.13<\sigma^2 < 4.91`

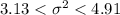
Explanation:

We are given the following in the question:

Sample size, n = 67

Variance = 3.85

We have to find 80% confidence interval for the population variance of the weights.

Degree of freedom = 67 - 1 = 66

Level of significance = 0.2

Chi square critical value for lower tail =

`\chi^2_{1-(\alpha)/(2)}= 51.770`

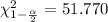
Chi square critical value for upper tail =

`\chi^2_{(\alpha)/(2)}= 81.085`

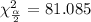
80% confidence interval:

`\frac{(n-1)S^2}{\chi^2_{(\alpha)/(2)}} < \sigma^2 < \frac{(n-1)S^2}{\chi^2_{1-(\alpha)/(2)}}`

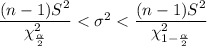
Putting values, we get,

`=((67-1)3.85)/(81.085) < \sigma^2 < ((67-1)3.85)/(51.770)\\\\=3.13<\sigma^2 < 4.91`

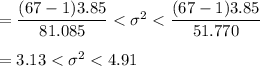
Thus, (3.13,4.91) is the required 80% confidence interval for the population variance of the weights.