Question

2. Calculate the thermal velocity of electrons in a conductor, taking that their kinetic energy equals the thermal energy kkBBTT with kB being the Boltzmann constant, at the following temperatures: a. 100 K b. 300 K c. 1000 K Compare the velocities you obtained in each answer to the speed of light.

Answer 1

(a).
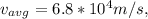`v_(avg) = 6.8*10^(4)m/s,` is 0.02% the speed of light.

(b).
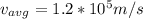`v_(avg) = 1.2*10^5m/s`, is 0.04% the speed of light.

(c).
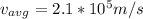`v_(avg) =2.1*10^5m/s` is 0.07% the speed of light.

Step-by-step explanation:

The average kinetic energy is related to the thermal energy of the electrons in a conductor by the the relation

`K.E_(avg) = (1)/(2)mv_(avg)^2 = (3)/(2)kT`,

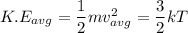where
`m = 9.1*10^(-31)kg` is the mass of the electrons,
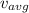`v_(avg)` is their average velocity,
`T` is the temperature of the conductor, and
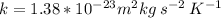`k = 1.38*10^(-23)m^2kg \:s^(-2)\:K^(-1)` is the Boltzmann constant.

The equation, when solved for
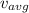`v_(avg)`, gives

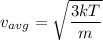
`v_(avg) = \sqrt{(3kT)/(m) }`

(a),

For
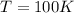`T = 100K`, the thermal (average) velocity
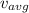`v_(avg)` is

`v_(avg) = \sqrt{(3(1.38*10^(-23))(100K))/(9.1*10^(-31)kg) }`

`\boxed{v_(avg) = 6.8*10^(4)m/s}`

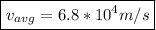
which when compared to the speed of light is

`(6.8*10^4)/(3*10^8) *100\% = (0.02\%)c`

0.02% the speed of light.

(b).

Similarly, for
`T =300K`

`v_(avg) = \sqrt{(3(1.38*10^(-23))(300K))/(9.1*10^(-31)kg) }`

`\boxed{v_(avg) = 1.2*10^5m/s}`

which is

`(1,2*10^5m/s)/(3*10^8m/s) *100\%= (0.04\%)c`

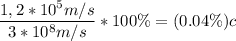
0.04% the speed of light.

(c).

Finally, for
`T =1000K`

`v_(avg) = \sqrt{(3(1.38*10^(-23))(1000k))/(9.1*10^(-31)kg) }`

`\boxed{v_(avg) =2.1*10^5m/s}`

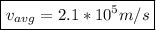
which is

`(2.1*10^5m/s)/(3*10^8m/s) *100\% = (0.07\%)c`

0.07% the speed of light.

We see that the average electron velocities we obtain are always less than 1% the speed of light, which means relativistic effects are negligible, for they are apparent at about 25% the speed of light.