Answer:
The number c=
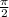 satisfies conclusion of Roller's theorem.
satisfies conclusion of Roller's theorem.
Explanation:
Given function is,
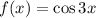 which is,
which is,
(1) continuous on the closed interval
![\Big[(\pi)/(12),(7\pi)/(12)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/c1nl76bu64l2inipvg7u3w66t6stiomhew.png) . Since,
. Since,
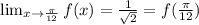 and,
and,
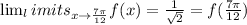
(2) derivable in the open interval
![\Big[(\pi)/(12),(7\pi)/(12)\Big]](https://img.qammunity.org/2021/formulas/mathematics/college/c1nl76bu64l2inipvg7u3w66t6stiomhew.png) because of continuity.
because of continuity.
(3)
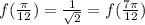
Hence all conditions of Rollr's theorem satisfied, so there exist at least one value c, where
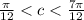 such that,
such that,
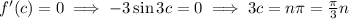 where n is an integer.
where n is an integer.
When,
n=1, c=

n=2, c=
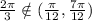
Similarly for other values of n, c lies outside of the given interval.
Hence c=
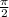 satisfies conclusion of Roller's theorem.
satisfies conclusion of Roller's theorem.