Question

A University of Arkansas student running for president of her sorority wanted to identify the issues are most important to the members of her sorority. To do so, she created a survey that asks various questions concerning the sorority. Thirty-seven out of 120 members completed the survey. The first question on the survey asked the members to rate the quality of food provided in the sorority house. The answers can range from 1 (very poor) to 5 (very good). The second question asked the members to state the total number of hours they individually volunteered during the semester. A 95% confidence interval showed the lower limit to be 10 hours and the upper limit to be 20 hours. What is the margin of error?

Answer 1

The margin of error is 5 hours.

Explanation:

A (1 - α)% confidence interval for the population mean μ is:

`CI=\bar x\pm CV * SE_(\bar x)`

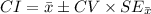
The margin of error is a numerical value representing the difference between the true parameter value and the sample statistic value.

In the confidence interval for the population mean μ the margin of error is:

`MOE=CV* SE_(\bar x)`

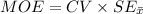
OR

`MOE=(Width)/(2)=(Upper\ limit-Lower\ limit)/(2)`

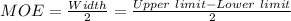
The 95% confidence interval for the mean number of hours spent volunteering during the semester is, (10, 20).

The width of the interval is:

Width = Upper limit - Lower limit

= 20 - 10

= 10

Compute the margin of error as follows:

`MOE=(Width)/(2)=(10)/(2)=5`

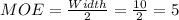
Thus, the margin of error is 5 hours.