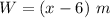Question

The rectangle below has an area of x^2−4x−12, squared, minus, 4, x, minus, 12 square meters and a length of x+2x+2 x+2 x, plus, 2 meters. What expression represents the width of the rectangle?

Answer 1

`W=(x-6)\ m`

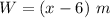
Explanation:

we know that

The area of rectangle is given by the formula

`A=LW`

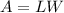
we have

`A=(x^2-4x-12)\ m^2`

`L=(x+2)\ m`

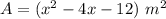
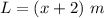
substitute

`x^2-4x-12=(x+2)W`

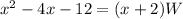
Solve the quadratic equation of the left side

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

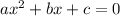
is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`x^2-4x-12=0`

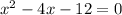
so

`a=1\\b=-4\\c=-12`

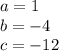
substitute in the formula

`x=\frac{-(-4)\pm\sqrt{-4^(2)-4(1)(-12)}} {2(1)}`

`x=\frac{4\pm√(64)} {2}`

`x=\frac{4\pm8} {2}`

`x=\frac{4+8} {2}=6`

`x=\frac{4-8} {2}=-2`

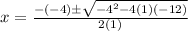
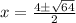
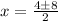
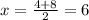
therefore

`x^2-4x-12=(x+2)(x-6)`

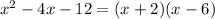
substitute in the formula of area

`(x+2)(x-6)=(x+2)W`

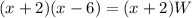
solve for W

simplify

`W=(x-6)\ m`