Question

An isosceles triangle whose equal sides measure 8 and whose altitude drawn to the base measures 8

Answer 1

The question is incomplete, the complete question is here

Find the measures of the angles of an isosceles triangle whose equal sides measure 8 and whose altitude drawn to the base measures 4

Answer:

The measures of the angles of the isosceles triangle are 30°, 30° and 120°

Explanation:

In a triangle whose sides a, b, c and angles A, B and C, where a is opposite to ∠A, b is opposite to ∠B, and c is opposite to ∠C, the given is

• a = c
• m∠A = m∠C

The height from ∠B to side b is 4 units

That means the length of the height is half the length of each equal sides, then there is a right triangle its hypotenuse is 8 and the side opposite to the base angle is 4, so we can find the measure of the base angle by using the rule sin(base angle) =
`(altitude)/(a)`

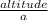
∵ The base angles are ∠A and ∠C

∵ a = c = 8

∵ The altitude to b is 4

∵
`sin(A)=(4)/(8)=(1)/(2)`

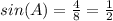
- By using
`sin^(-1)`

∴ m∠A =
`sin^(-1)((1)/(2))`

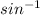
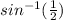
∴ m∠A = 30°

∵ m∠A = m∠C

∴ m∠C = 30°

Use the rule of the sum of the measures of the interior angle of a Δ is 180° to find m∠B

∵ m∠A + m∠C + m∠B = 180

∵ m∠A = m∠C = 30°

∴ 30° + 30° + m∠B = 180°

∴ 60 + m∠B = 180

- Subtract 60 from both sides

∴ m∠B = 120°

The measures of the angles of the isosceles triangle are 30°, 30° and 120°