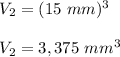Question

bicycle, A company that makes dice (cube), is looking to change The size of the days they produce. The current days have edge length of 5mm, in the company wants to increase them to 15mm. how will the volume of the day to be affected if this changes made?

Answer 1

Answer: If that change is made, the new volume will be
`3,375\ mm^3`

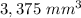
Explanation:

For this exercise it is important to remember that the formula used to calculate the volume of a cube is the following:

`V=s^3`

Where "s" is the lenght of any edge of the cube.

You know that the current days have edge length of 5 mm.

Then, knowing the formula for calculate the volume of a cube, you get that the current volume of any of those cubes made by the company is:

`V_1=(5\ mm)^3\\\\V_1=125\ mm^3`

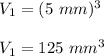
Since they want to increase the length to 15 mm, you can identify that:

`s=15\ mm`

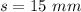
Therefore, knowing this new edge you can calculate the new volume.

You get that this is:

`V_2=(15\ mm)^3\\\\V_2=3,375\ mm^3`