(A) The mean is 82
(B) The mean absolute deviation is approximately 9.71
(D) The IQR is 11
Step-by-step explanation:
(A) 89, 87, 54, 78, 87, 99, 80
Mean of the data =
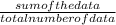
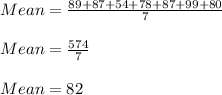
Therefore, mean of the data is 82
(B) The mean absolute deviation, MAD is
data - 54, 78, 80, 87, 87, 89, 99
Mean of the data, x' is 82
|x - x'| : 54 - 82 = 28
78 - 82 = 4
80 - 82 = 2
87 - 82 = 5
87 - 82 = 5
89 - 82 = 7
99 - 82 = 17
Total of |x - x'| = 68
MAD = |x - x'| / n
MAD = 68/7
MAD = 9.71
(D) IQR is the interquartile range
Data = 54, 78, 80, 87, 87, 89, 99
IQR = median of lower quartile range - median of upper quartile range
IQR = 89 - 78
IQR = 11