Question

PLEASE HELP ME!!!!! The object above is symmetrical through z. If x = 8 inches, y = 11 inches, and h = 7 inches, what is the perimeter of the object?

A. 52 inches

B. 45 inches

C. 26 inches

D. 38 inches

Answer 1

38in

Explanation:

2x+2y=2x8+2x11=16+22=38 in

Answer 2

The perimeter of the object is 38 inches. Hence, option D is correct.

The object you described can be modeled as two right triangles, ABE and ADE, sharing a common side AE. Since the object is symmetrical through z, we can assume that triangles ABE and ADE are congruent.

Now, we can use the given information to solve for the missing side lengths:

* We are given that `x = 8` inches and `y = 11` inches, which are the hypotenuse of triangles ABE and ADE, respectively.

* We are also given that `h = 7` inches, which is the height of both triangles (since BC is the perpendicular bisector of AE).

Using the Pythagorean theorem, we can find the base of each triangle:

* For triangle ABE:
`z_1^2 = y^2 - h^2 = 11^2 - 7^2 = 84`

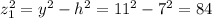
* So,
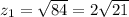`z_1 = √(84) = 2√(21)$` inches (since z must be positive).

Since the triangles are congruent, the base of triangle ADE (
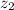`z_2`) is also equal to
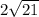`2√(21)$` inches.

Finally, to find the perimeter of the object, we simply add up the lengths of all sides:

* Perimeter =
`x + z_1 + y + z_2`

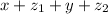
* Perimeter = 8 +
`2√(21) + 11 + 2√(21)`

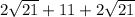
* Perimeter =
`19 + 4√(21) \approx 38.97` inches (rounded to two decimal places)

Therefore, the answer is D) 38 inches.