Question

A square loop of side 7 cm is placed with the nearest side 2 cm from a long wire carrying a current that varies with time at a constaent rate of 9 A/s. (Assume the loop and the wire lie in the same plane. Further assume I- 0at t 0. Enter the magnitudes.) (a) Use Ampère's law and find the magnetic feld from the current in the wire as a function of time and dstance from the wire. (Use the folowing as necessary: j is in meters and t is in seconds. Do not include units in your answer) , and t. Assume 8 is in teslas, r Br, t) (b) Determine the magnetic flux through the loop. (Use the following as necessary: and t. Assume is in T m and t is in seconds. Do not include units in your answer) (c) If the loop has a resistance of 3 0, how much induced current flows in the loop (in nA)) nA

Answer 1

Step-by-step explanation:

side of the square loop, a = 7 cm

distance of the nearest side from long wire, r = 2 cm = 0.02 m

di/dt = 9 A/s

Integrate on both the sides

`\int _(0)^(i)di =9\int _(0)^(t)dt`

i = 9t

(a) The magnetic field due to the current carrying wire at a distance r is given by

`B = (\mu_(0)i)/(2\pi r)`

`B = (\mu_(0)* 9t)/(2\pi r)`

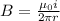
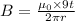
(b)

Magnetic flux,

`\phi=\int B* a dr`

`\phi=\int (\mu_(0)* 9t)/(2\pi r)* a dr`

`\phi=(\mu_(0)* 9t* a)/(2\pi)* ln\left ( (2 + 7)/(2) \right )`

`\phi=(\mu_(0)* 9t* 0.07)/(2\pi)* ln(4.5)`

`\phi = 1.89 * 10^(-7)t`

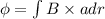
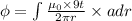
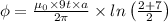
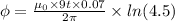
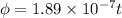
(c)

R = 3 ohm

`e = -(d\phi)/(dt)`

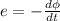
magnitude of voltage is

e = 1.89 x 10^-7 V

induced current, i = e / R = (1.89 x 10^-7) / 3

i = 6.3 x 10^-8 A