Question

Among all rectangles that have a perimeter of 182, find the dimensions of the one whose area is largest.

Answer 1

The largest rectangle of perimeter 182 is a square of side 45.5

Explanation:

Maximization Using Derivatives

The procedure consists in finding an appropriate function that depends on only one variable. Then, the first derivative of the function will be found, equated to 0 and find the maximum or minimum values.

Suppose we have a rectangle of dimensions x and y. The area of that rectangle is:

`A=x.y`

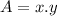
And the perimeter is

`P=2x+2y`

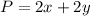
We know the perimeter is 182, thus

`2x+2y=182`

Simplifying

`x+y=91`

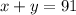
Solving for y

`y=91-x`

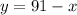
The area is

`A=x.(91-x)=91x-x^2`

Taking the derivative:

`A'=91-2x`

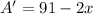
Equating to 0

`91-2x=0`

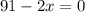
Solving

`x=91/2=45.5`

Finding y

`y=91-x=45.5`

The largest rectangle of perimeter 182 is a square of side 45.5