Question

18. Manufacturers often package products in a way that uses the least amount of material One measure of the efficiency of a package is the ratio of its surface area to its volume. The smaller the ratio, the more efficient the packaging. A company makes a cylindrical can to hold popcorn. The company is designing a new can with the same height h and twice the radius r of the old can. a. Write an expression for the efficiency ratio where S is the surface area of the can and Vis the volume of the can. b. Find the efficiency ratio for each can. c. Did the company make a good decision by creating the new can? Explain

Answer 1

a.
`E=(2h+2r)/(rh)`

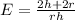
b.

E of first can =
`E=(2h+2r)/(rh)`

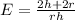
E of second can =
`E=(h+2r)/(rh)`

c. Yes

Explanation:

The efficiency ratio is:

E = Surface Area / Volume

a.

We can write:

`E=(S)/(V)`

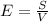
Where

S is surface area of cylinder

V is volume of cylinder

The formulas are:

S =
`2\pi rh+2\pi r^2`

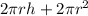
V =
`\pi r ^2 h`

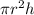
So, the efficiency ratio (E) is:

`E=(2\pi rh+2\pi r^2)/(\pi r^2 h)\\E=(\pi r(2h+2r))/(\pi r(rh))\\E=(2h+2r)/(rh)`

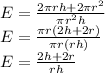
b.

The first can has radius "r" and height "h", so the efficiency ratio is:

`E=(S)/(V)\\E=(2\pi rh+2\pi r^2)/(\pi r^2 h)\\E=(\pi r(2h+2r))/(\pi r(rh))\\E=(2h+2r)/(rh)`

The second can has same height, "h", and twice radius, "2r", so the efficiency ratio becomes:

`E=(S)/(V)\\E=(2\pi (2r)h+2\pi (2r)^2)/(\pi (2r)^2 h)\\E=(4\pi rh +8\pi r^2)/(4\pi r^2h)\\E=(4\pi r(h+2r))/(4\pi r(rh))\\E=(h+2r)/(rh)`

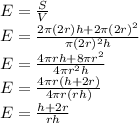
c.

We now need to say if the company made a good decision or not.

If you look at both the Efficiency ratios above, you will see that the difference is in the numerator.

The first can has "2h"

The second can has "h"

The "2h" makes the numerator for the first can BIGGER than the "h" of the second can, so the Efficiency ratio of first can is thus, BIGGER.

We need smaller ratio.

So, 2nd can has indeed smaller ratio, so the company made a good decision.