Answer:
The complete solution is

Explanation:
Given differential equation is
3y"- 8y' - 3y =4
The trial solution is
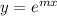
Differentiating with respect to x
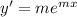
Again differentiating with respect to x

Putting the value of y, y' and y'' in left side of the differential equation
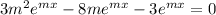
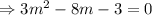
The auxiliary equation is
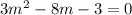
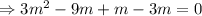
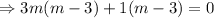
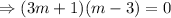
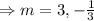
The complementary function is
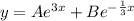
y''= D², y' = D
The given differential equation is
(3D²-8D-3D)y =4
⇒(3D+1)(D-3)y =4
Since the linear operation is
L(D) ≡ (3D+1)(D-3)
For particular integral
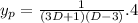
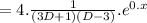 [since
[since
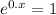 ]
]
 [ replace D by 0 , since L(0)≠0]
[ replace D by 0 , since L(0)≠0]

The complete solution is
y= C.F+P.I
