Question

The average reading speed of students completing a speed-reading course is 435 words per minute (wpm). If the standard deviation is 60 wpm, find the z-score associated with the following reading speeds then interpret the result. Round to two decimal places. a. 340 wpmb. 475 wpmc. 420wpmd. 610wpm

Answer 1

a)

`Z = -1.58`

Z = -1.58 means that a reading speed of 340 wpm is 1.58 standard deviations below the mean reading speed.

b)

`Z = 0.67`

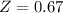
Z = 0.67 means that a reading speed of 475 wpm is 0.67 standard deviations above the mean reading speed.

c)

`Z = -0.25`

Z = -0.25 means that a reading speed of 420 wpm is 0.25 standard deviations below the mean reading speed.

d)

`Z = 2.92`

Z = 2.92 means that a reading speed of 610 wpm is 2.92 standard deviations above the mean reading speed.

Explanation:

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The z-score measures how many standard deviations a measure X is above or below the mean.

In this problem, we have that:

`\mu = 435, \sigma = 60`

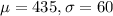
a. 340 wpm

`Z = (X - \mu)/(\sigma)`

`Z = (340 - 435)/(60)`

`Z = -1.58`

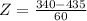
Z = -1.58 means that a reading speed of 340 wpm is 1.58 standard deviations below the mean reading speed.

b. 475 wpm

`Z = (X - \mu)/(\sigma)`

`Z = (475 - 435)/(60)`

`Z = 0.67`

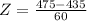
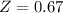
Z = 0.67 means that a reading speed of 475 wpm is 0.67 standard deviations above the mean reading speed.

c. 420wpm

`Z = (X - \mu)/(\sigma)`

`Z = (420 - 435)/(60)`

`Z = -0.25`

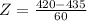
Z = -0.25 means that a reading speed of 420 wpm is 0.25 standard deviations below the mean reading speed.

d. 610wpm

`Z = (X - \mu)/(\sigma)`

`Z = (610 - 435)/(60)`

`Z = 2.92`

Z = 2.92 means that a reading speed of 610 wpm is 2.92 standard deviations above the mean reading speed.