Question

An electrical rm manufactures light bulbs that have a life span that is approximately normally distributed. The population standard deviation is not known. A sample of 30 bulbs are found to have an average life span of 800 hours and a sample standard deviation of 45 hours. Test the hypothesis that µ = 800 against the alternative µ ≠ 800 if a random sample of 30 bulbs has an average life 788 hours. Use P value in your answer.

Answer 1

The 't' test statistic = 1.46 < 1.69

The test of hypothesis is H 0 :μ = 800 is accepted

A sample of 30 bulbs are found came from average µ= 800

Explanation:

Step 1:-

Given population of mean μ = 800

given size of small sample n =30

sample standard deviation 'S' = 45

Mean value of the sample χ = 788

Null hypothesis
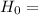`H_(0) =`µ =800

alternative hypothesis
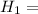`H_(1) =` µ ≠ 800

Step 2:-

The 't' test statistic t =
`(x-μ)/((sig)/(√(n) ) )`

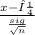
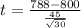
`t = (788-800)/((45)/(√(30) ) )`

t =
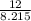`(12)/(8.215)` = 1.4607

Step 3:-

The degrees of freedom γ = n-1 = 30-1 =29

From "t" value from table at 0.05 level of significance ( t = 1.69)

The calculated value t = 1.4607 < 1.69

Therefore The null hypothesis H_{0} ' is accepted.

conclusion:-

A sample of 30 bulbs are came found from average µ= 800