Question

A projectile is launched from ground level at an angle of 30 degrees above the horizontal. Neglect air resistance and consider the motion from just after the moment it is launched to just before the moment it lands on the ground. When does the projectiles velocity equal its launch velocity?At the highest point.  The projectile's velocity is never equal to its launch velocity after launch.  The projectile's velocity is always equal to its launch velocity.  Just before landing on the ground.  Halfway back to the ground.  Halfway to the highest point.

Answer 1

just before landing the ground

Step-by-step explanation:

Let the velocity of projection is u and the angle of projection is 30°.

Let T is the time of flight and R is the horizontal distance traveled. As there is no force acting in horizontal direction, so the horizontal velocity remains constant. Let the particle hits the ground with velocity v.

initial horizontal component of velocity, ux = u Cos 30

initial vertical component of velocity, uy = u Sin 30

Time of flight is given by

`T = (2u Sin\theta )/(g)`

Final horizontal component of velocity, vx = ux = u Cos 30

Let vy is teh final vertical component of velocity.

Use first equation of motion

vy = uy - gT

`v_(y)=u_(y)- g * (2u Sin\theta )/(g)`

`v_(y)=u Sin 30 - 2u Sin 30`

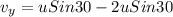
vy = - u Sin 30

The magnitude of final velocity is given by

`v = \sqrt{v_(x)^(2)+v_(y)^(2)}`

`v = \sqrt{\left (uCos 30 \right )^(2)+\left (uSin 30 \right )^(2)}`

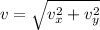
v = u

Thus, the velocity is same as it just reaches the ground.