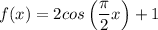Question

Can someone help me write an equation for a graph as shown in the image, midline 1 period 4 amplitude 2

Answer 1

`\displaystyle f(x)=2cos\left( (\pi)/(2)x\right)+1`

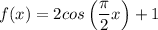
Midline:1

Amplitude: 2

Period: 4

Explanation:

Equation of a Cosine

The general equati of of the cosine is

`f(x)=A.cos(wx+\phi)+M`

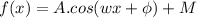
With the following parameters:

A=Amplitude or half the length from the maximum to the minimum values

w=angular frequency (rad/sec)

`\phi`=phase shift (rad or degrees)

M=Midline of vertical shift.

The cosine and the sine are both sinusoid functions but we have chosen the cosine as the selected function because its value is maximum when x=0, just like the graph shown in the question.

It can be seen that the maximum value is 3 and the minimum value is -1. That gives us the amplitude:

`\displaystyle A=(3+1)/(2)=2`

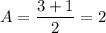
The midline can be found as the displacement from the center of the wave. Since the maximum value is 3 and the amplitude is 2, the midline is

`M=3-2=1`

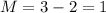
The general equation is now

`f(x)=2cos(wx+\phi)+1`

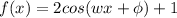
To compute the phase shift and the angular frequency, we take two points from the graph: (0,3) (4,3). Let's plug in both values:

`f(0)=2cos(w(0)+\phi)+1=3`

`2cos\phi=2`

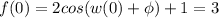
Solving

`cos\phi=1`

`\phi=0`

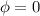
The equation is now

`f(x)=2cos(wx)+1`

Now for the next point

`f(4)=2cos(w\cdot 4)+1=3`

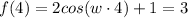
2cos(4w)=2

cos(4w)=1

The solution for the equation cannot be an angle of 0, we go forward to the next angle where the cosine is 1

`4w=2\pi`

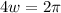
Or, equivalently

`\displaystyle w=(\pi)/(2)`

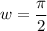
The period is given by

`\displaystyle T=(2\pi)/(w)`

`\displaystyle T=(2\pi)/((\pi)/(2))=4`

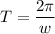
The equation of the function is

`\displaystyle f(x)=2cos\left( (\pi)/(2)x\right)+1`