Answer:
heya! ^^
here , we've been given a right angled triangle along with the measure of two of its sides.
and , we've to find the measure of its third side.
so , we'll be using Pythagoras Theorem to find the measure of the third side.
but first , let's take a look at what Pythagoras Theorem is-
Pythagoras theorem states that the square of the hypotenuse of the triangle is equal to the sum of squares of the remaining two sides.
according to the figure ,
side AB = hypotenuse = 60 cm
side AC = perpendicular = 48 cm
side BC = base = a
now by using Pythagoras Theorem ,
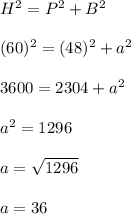
therefore ,
option ( 4 ) 36 is correct.
hope helpful :D