Question

Sarah took the advertising department from her company on a round-trip to meet with a potential client including Sarah a total of 13 people took the trip she was able to purchase Coach tickets for $260 in first class tickets for $1080 she used her total budget for airfare for the trip which was $9940 how many first class tickets did she buy how many coach tickets did she buy

Answer 1

-5 coach tickets

-8 first class tickets

Explanation:

let x be the number of coach tickets and y the number of first class tickets:

`x+y=13\ \ \ \ \ \ ...i`

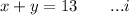
Given that coach tickets costs $260 each, and first class tickets $1080 and that the total fare budget was $9940:

`260x+1080y=9940\ \ \ \ \ \ \ \ \ ...ii`

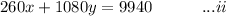
#From equation i, make x the subject of the formula:

`x=13-y`

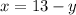
#Substitute x in ii;

`260x+1080y=9940\\\\260(13-y)+1080y=9940\\\\3380-260y+1080y=9940\\\\820y=6560\\\\y=8\\\\x=13-y\\\\\therefore x=13-8=5`

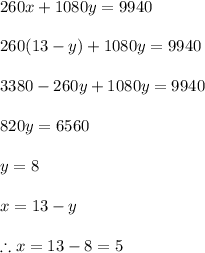
Hence, Sarah bought 5 coach tickets and 8 first class tickets.