Question

A production process produces 1.5% defective parts. A sample of six parts from the production process is selected. What is the probability that the sample contains exactly two defective parts?

Answer 1

`P(X=2)=0.003177`

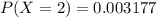
Explanation:

-Defective parts are modeled using a binomial probability function:

`P(X=x)={n\choose x}p^x(1-p)^x`

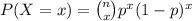
Where p is the probability of defects, n the sample size and x the sample space.

#Given the sample size as 6 and p=0.015, the probability that the sample contains exactly two defective parts is:

`P(X=x)={n\choose x}p^x(1-p)^x\\\\P(X=2)={6\choose 2}0.015^2(1-0.015)^4\\\\=0.003177`

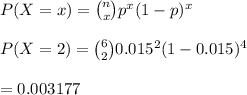
Hence, the probability that the sample contains exactly two defective parts is 0.003177