Question

Fiona plans to make a box in the shape of a rectangular prism for storing her outdoor checkers pieces and the

checker board. In order to fit all of the pieces, the box will need to have a volume of 96 cubic feet. The place she
needs to store it only has a height of 2 feet. She comes up with two different designs for the box. One of the
designs has dimensions of:
2 feet high by 6 feet wide by 8 feet long
A. What could be the dimension, in feet, of Fiona's other box design? Why does this meet Fiona's
requirements? (Hint: The volume of a rectangular prism is lwh.) SHOW and EXPLAIN your work.
Dimensions of other box design:

Answer 1

see the explanation

Explanation:

we know that

The volume of the rectangular prism is given by

`V=LWH`

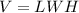
The box will need to have a volume of 96 cubic feet and a height of 2 feet

so

First design

we have

`L=8\ ft\\W=6\ ft\\H=2\ ft`

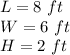
substitute the values

`V_1=(8)(6)(2)=96\ ft^3`

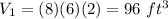
The first design meet Fiona's requirements

Second design

we have

`V=96\ ft^3\\H=2\ ft`

substitute in the formula

`96=(LW)(2)`

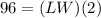
Solve for (LW)

`LW=96/2\\LW=48\ ft^2`

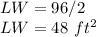
The area of the base must be equal to 48 square feet

We could have the following dimensions for L and W (the volume and the height are given)

12 feet by 4 feet ----> the base's area is equal to 48 square feet

16 feet by 3 feet ----> the base's area is equal to 48 square feet

2 feet by 24 feet ----> the base's area is equal to 48 square feet

4√3 feet by 4√3 ---> the base's area is equal to 48 square feet

All the above dimensions meet Fiona's requirements

therefore

The dimensions of the second design could be

2 feet high by 4 feet wide by 12 feet long

2 feet high by 3 feet wide by 16 feet long

2 feet high by 2 feet wide by 24 feet long

2 feet high by 4√3 feet wide by 4√3 feet long