Question

HELP ASAP

Is this exponential growth or decay? y= x(1/3)^x+1

What are the transformations

Answer 1

a) Exponential decay

b,) The parent function is shifted up 1 unit.

Explanation:

Assuming your function is

`y = ( (1)/(3) )^(x) + 1`

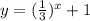
Then we can compare this to:

`y = {b}^(x) + c`

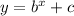
If

`0 \: < \: b \: < 1`

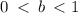
then y is an exponential decay function.

If |b|>1, then y is an exponential growth.

We can see that:

`0 \: < \: (1)/(3) \: < \: 1`

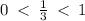
Therefore the given function is an exponential decay.

The parent function is shifted up 1 unit.