Question

For a portion of the Green River in Utah, the rate of the river's current is 4 mph. A tour guide can row 5 mi down this river and back in 3 h. Find the rowing rate of the guide in calm water.

Answer 1

Rowing rate of the guide in calm water is 6 mph.

Explanation:

Let the rowing rate of the guide is x mph in the calm water.

Rate of river's current = 4 mph

Therefore, speed of the boat upstream = (x - 4) mph

and speed of the river downstream = (x + 4) mph

Time taken to row 5 miles upstream =
`\frac{\text{Distance traveled}}{\text{speed}}`

=
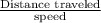
`(5)/((x-4))` hours

Time taken to row 5 miles downstream =
`(5)/((x+4))` hours

Since total time spent to row down and come back is = 3 hours

So
`(5)/((x-4))+(5)/((x+4))=3`

`5[(x+4+x-4)/((x-4)(x+4))]=3`

5(2x) = 3(x - 4)(x + 4)

10x = 3(x² - 16)

3x² - 10x - 48 = 0

From quadratic formula,

x =
`\frac{-b\pm \sqrt{b^(2)-4ac}}{2a}`

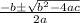
From our equation,

a = 3, b = -10 and c = -48

Now we plug in these values in the formula,

x =
`\frac{10\pm \sqrt{(-10)^(2)-4(3)(-48)}}{2(3)}`

=
`(10\pm √(100+576) )/(6)`

=
`(10\pm √(676))/(6)`

=
`(10\pm 26)/(6)`

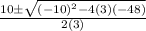
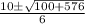
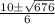
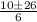
= 6, -2.67 mph

Since speed can not be negative so x = 6 mph will be the answer.

Therefore, rowing rate of the guide in calm water is 6 mph.