Answer:
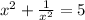
Explanation:
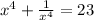 is given.
is given.
We want to find
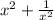 .
.
If we square the value we want to find, we should wind up with some terms of the left hand side of the given.
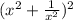
Expand:
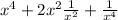 (We used the identity:
(We used the identity:
 for expansion).
for expansion).
Simplify this value:
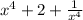
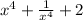
We are given that the sum of the first two terms is 23.
This means
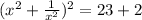 .
.
Let's simplify the right hand side.

Now to find the value we want we must simply take the square root of both sides.
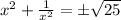
Simplify the right hand side:
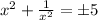
Since
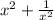 is positive for any real value
is positive for any real value
 (that is not zero), then we can conclude
(that is not zero), then we can conclude
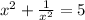 .
.