Question

IA triangular parking lot is paved outside a new shopping center. The lengths of the sides of the parking lot are 100 meters, 113 meters, and 86 meters. What is the area of the parking lot..Step by step explanation..Please..

Answer 1

Explanation:

I believe the only way to solve this is by Heron's Formula.

Add up all the sides and divide by 2 to get the semi-perimeter:

113+100+86 = 299

299/2 = 149.5

Now fill in the rest, which looks like this:

`√(s(s-a)(s-b)(s-c))`

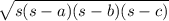
where s is your semiperimeter value, a is the length of one side, b the length of another side, and c the length of the third side:

`√(149.5(149.5-113)(149.5-100)(149.5-86))`

which simplifies to

`√(149.5(36.5)(49.5)(63.5))`

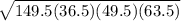
which simplifies further to

`√(17151929.44)`

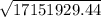
which, on your calculator, is 4141.49 meters squared (that's rounded to the nearest hundredth).