Question

1) If the alpha level is changed from α = .05 to α = .01, what happens to boundaries for the critical region?

The boundaries:

a. Move farther into the tails
b. Move closer to the center
c. Do not move

2) What happens to the probability of a Type I error when the alpha level is changed from α = .05 to α = .01?
The probability:

a. Decreases
b. Remains Constant
c. Increases

Answer 1

Changing the alpha level from .05 to .01 moves critical region boundaries farther into the tails and decreases the probability of a Type I error because the criteria for rejecting the null hypothesis become more stringent. So Correct options are 1->a and 2->a

Step-by-step explanation:

When the alpha level is changed from α = .05 to α = .01, the boundaries for the critical region move farther into the tails of the distribution. This is because a lower alpha level means that you require more extreme evidence to reject the null hypothesis, hence the critical values are further from the center of the distribution.

As for the probability of a Type I error, when the alpha level is changed from α = .05 to α = .01, the probability decreases. A Type I error is the probability of incorrectly rejecting a true null hypothesis. Therefore, by making the alpha level smaller, you are making the criteria for rejection more stringent and hence less likely to commit a Type I error.

Answer 2

1) a. Move farther into the tails

2) a. Decreases

Step-by-step explanation:

Hello!

1)

Let's say for example that you are making a confidence interval for the mean, using the Z-distribution:

X[bar] ±
`Z_(1-\alpha /2)` *
`(Sigma)/(√(n) )`

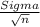
Leaving all other terms constant, this are the Z-values for three different confidence levels:

90%
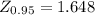
`Z_(0.95)= 1.648`

95%
`Z_(0.975)= 1.965`

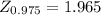
99%
`Z_(0.995)= 2.586`

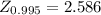
Semiamplitude of the interval is

d=
`Z_(1-\alpha /2)` *
`(Sigma)/(√(n) )`

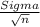
Then if you increase the confidence level, the value of Z increases and so does the semiamplitude and amplitude of the interval:

↑d= ↑
`Z_(1-\alpha /2)` *
`(Sigma)/(√(n) )`

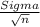
They have a direct relationship.

So if you change α: 0.05 to α: 0.01, then the confidence level 1-α increases from 0.95 to 0.99, and the boundaries move farther into the tails.

2)

The significance level of a hypothesis test is the probability of committing a Type I error.

If you decrease the level from 5% to 1%, then logically, the probability decreases.

I hope this helps!