Question

Two solenoids have the same cross-sectional area and length, but the first one has twice as many turns er unit length as the second.

The ratio of the self-inductance of the second solenoid to that of the first is :

a. 1:2

b. 1:4

c. 2:1

d. 4:1

e. 1:1

Answer 1

option (b)

Step-by-step explanation:

number of turns in the first solenoid, N1 = N

number of turns in the second solenoid, N2 = 2N

Let the current is i and the length is l and the area of crossection of the solenoid is A.

The formula for the self inductance of the solenoid is

`L=(\mu _(0)N^2* A)/(l)`

It means the self inductance of the solenoid is directly proportional to the square of number of turns.

So,
`(L_(1))/(L_(2))=(N^(2))/(4N^(2))`

L1 : L2 = 1 : 4

Answer 2

b:1:4

Step-by-step explanation:

We are given that two solenoid.

Suppose ,the length of each solenoid=l

Cross-sectional area of each solenoid=A

Let , number of turns in in second solenoid,
`N_2=N`

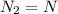
Number of turns in first solenoid,
`N_1=2 N`

We have to find the ratio of self-inductance of the second solenoid to that of the first.

Self- inductance,L=
`(\mu_0N^2A)/(l)`

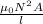
Using the formula

Self- inductance of one solenoid,
`L_1=(\mu_0(2N)^2A)/(l)=(\mu_04N^2A)/(l)`

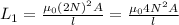
Self-inductance of second solenoid,
`L_2=(\mu_0N^2A)/(l)`

`(L_2)/(L_1)=(N^2)/(4N^2)=(1)/(4)`

`L_2:L_1=1:4`

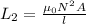
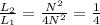
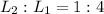
Hence, option b is true.