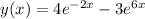Question

Given the second order homogeneous constant coefficient equation y′′−4y′−12y=0 1) the characteristic polynomial ar2+br+c is r^2-4r-12 . 2) The roots of auxiliary equation are (enter answers as a comma separated list). 3) A fundamental set of solutions is (enter answers as a comma separated list). 4) Given the initial conditions y(0)=1 and y′(0)=−26 find the unique solution to the IVP y= .

Answer 1

The initial value problem
`y(x) = 4 e^(-2x) -3 e^(6 x)`

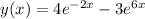
Explanation:

Step1:-

a) Given second order homogenous constant co-efficient equation

`y^(ll) - 4y^(l)-12y=0`

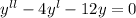
Given equation in the operator form is
`(D^(2) -4D-12)y=0`

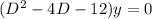
Step 2:-

b) Let f(D) =
`(D^(2) -4D-12)y`

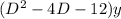
Then the auxiliary equation is
`(m^(2) -4m-12)=0`

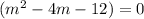
Find the factors of the auxiliary equation is

`m^(2) -6m+2m-12=0`

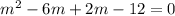
m(m-6) + 2(m-6) =0

m+2 =0 and m-6=0

m=-2 and m=6

The roots are real and different

The general solution
`y = c_(1) e^{-m_(1) x} + c_(2) e^{m_(2) x}`

the roots are
`m_(1) = -2 and m_(2) = 6`

The general solution of given differential equation is

`y = c_(1) e^(-2x) + c_(2) e^(6 x)`

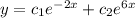
Step 3:-

C) Given initial conditions are y(0) =1 and y1 (0) =-26

The general solution of given differential equation is

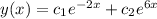`y(x) = c_(1) e^(-2x) + c_(2) e^(6 x)` .....(1)

substitute x =0 and y(0) =1

`y(0) = c_(1) e^(0) + c_(2) e^(0)`

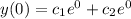
`1 = c_(1) + c_(2)` .........(2)

Differentiating equation (1) with respective to 'x'

`y^l(x) = -2c_(1) e^(-2x) + 6c_(2) e^(6 x)`

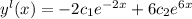
substitute x= o and y1 (0) =-26

`-26 = -2c_(1) e^(0) + 6c_(2) e^(0)`

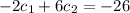`-2c_(1) + 6c_(2) = -26` .............(3)

solving (2) and (3) by using substitution method

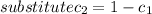`substitute c_(2) =1- c_(1)` in equation (3)

`-2c_(1) + 6(1-c_(1)) = -26`

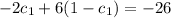
on simplification , we get

`-2c_(1) + 6(1)-6c_(1)) = -26`

`-8c_(1) = -32`

dividing by'8' we get
`c_(1) =4`

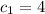
substitute
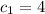`c_(1) =4` in equation
`1 = c_(1) + c_(2)`

so
`c_(2) = 1-4 = -3`

now substitute
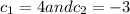`c_(1) =4 and c_(2) =-3` in general solution

`y(x) = c_(1) e^(-2x) + c_(2) e^(6 x)`

`y(x) = 4 e^(-2x) -3 e^(6 x)`

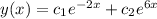
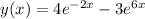
now the initial value problem

`y(x) = 4 e^(-2x) -3 e^(6 x)`