Question

A thief steals an ATM card and must randomly guess the correct six​-digit pin code from a 4​-key keypad. Repetition of digits is allowed. What is the probability of a correct guess on the first​ try?

Answer 1

The probability of a correct guess on the first​ try is 0.000244 or 0.0244%.

Explanation:

Given:

Number of digits in the pin code = 6

Number of keys in each digit = 4

So, in order to get the correct pin code, the key selected in each digit should be correct.

So, there will be only 1 correct key in each digit.

Now, probability of selecting a correct key in first digit is given as:

`P(correct\ key)=(Number\ of\ correct\ keys)/(Total\ number\ of\ keys)\\\\P(correct\ key)=(1)/(4)=0.25`

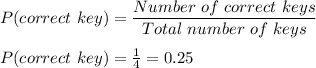
Now, there are 6 digits in the pin code and repetition is allowed. So, the probability of selecting the correct key in the remaining digits will also be equal to 0.25.

Therefore, the combined probability of selecting the correct pin code in the first try is the product of probabilities of selecting each correct key in each of the digits.

So,
`P(correct\ pin\ code)=(0.25)^6=0.000244`

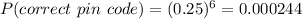
Therefore, the probability of a correct guess on the first​ try is 0.000244 or 0.0244%.