Answer:
The graph will increase at a slower rate
The y-values will continue to increase as x-increases
Explanation:
we have the exponential function
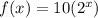
This is a exponential growth function, because the base of the exponential function is greater than 1 (b=2)
If the b value in the equation is decreased but remains greater than 1, the exponential equation will continue to be a exponential growth function
so
Verify each statement
1) The graph will begin at a lower point on the y-axis
The statement is false
Because, the graph will begin at the same initial value than the original function. The initial value for both cases is 10
2) The graph will increase at a faster rate.
The statement is false
Because, the graph will increase at a slower rate
3) The graph will increase at a slower rate.
The statement is true
Because, if the b value in the equation is decreased, the rate of change is decreased too
4) The y-values will continue to increase as x-increases
The statement is true
Because the function continue to be a exponential growth function
5) The y-values will each be less than their corresponding x-values
The statement is false
Because, the y-values will each be greater than their corresponding x-values