Answer:
85.71% probability that it takes Evelyn less than 38 minutes given that it takes less than 41 minutes for her to go grocery shopping
Explanation:
An uniform probability is a case of probability in which each outcome is equally as likely.
For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.
The probability that we find a value X lower than x is given by the following formula.
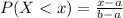
Uniformly distributed between 20 minutes and 44 minutes.
This means that
 .
.
What is the probability that it takes Evelyn less than 38 minutes given that it takes less than 41 minutes for her to go grocery shopping
We know that it takes less than 41 minutes, so we can update b to 41.
So
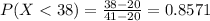
85.71% probability that it takes Evelyn less than 38 minutes given that it takes less than 41 minutes for her to go grocery shopping